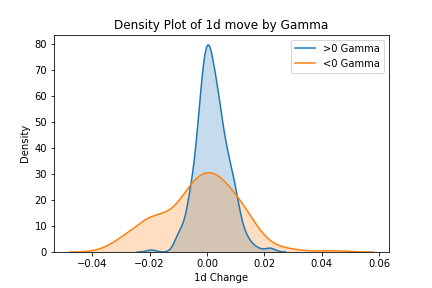
Following a LinkedIn blog(?) by a Deutsche Bank fellow who took issue with market gamma models, I decided to run a few quick simulations to look at model error. Many gamma models assume all calls are sold to dealers and all puts are bought from dealers. Certainly this cannot be 100% true, but the back data which uses these assumptions is statistically compelling . The blogger does not address any actual data produced via gamma modeling – for instance the chart below showing the 1 day SPX price distribution for positive vs negative gamma. (Note this data comes out pre-open).
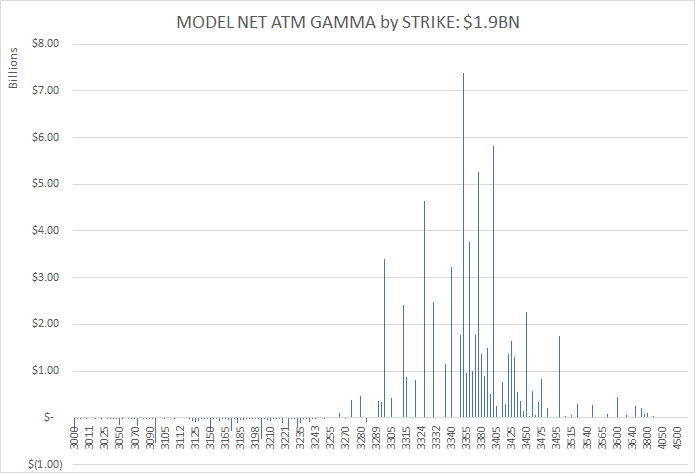
Using the most recent gamma data available (2/7/20) I used excel to visualize how different the gamma distribution may look if we assume that the model is only 50% correct – and the remaining 50% open interest is randomized to be long or short. Just below is our models “normal” chart, with three “random” graphs below that. You can see with those three “random” charts how much the gamma profile can change with a 50% adjustment.
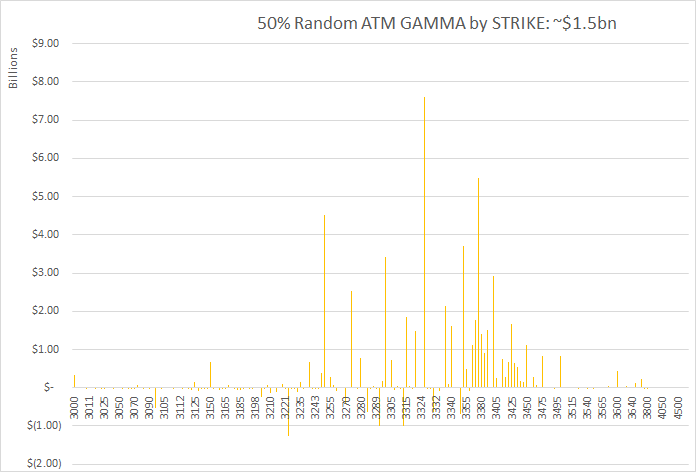
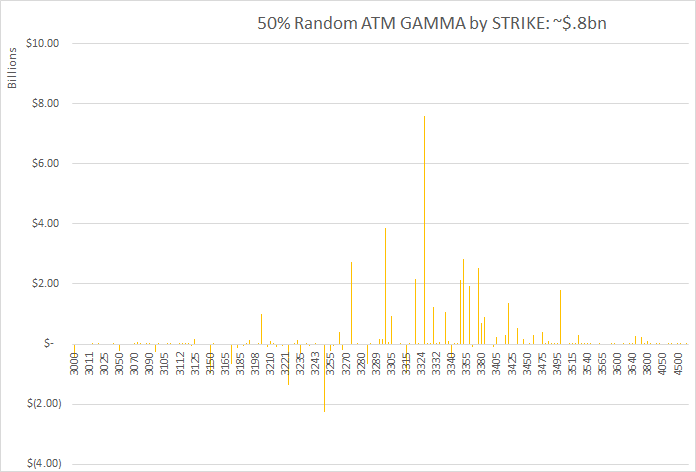
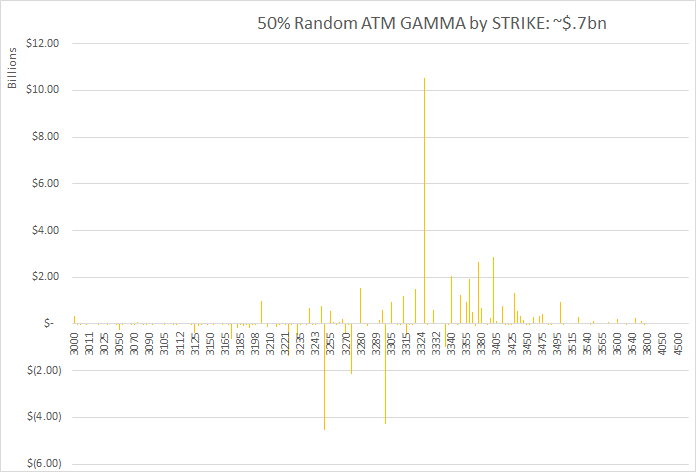
I then ran a simulation which stepped through adjusting the models assumption from 50-90%. Running 1,000 trails at 10% intervals from 50% to 90%. 70% for example uses 70% of our base assumptions and 30% randomized. This produced the following total gamma levels:
| Rate Adj. | Simulation Avg Gamma | Pct of Model |
| 50% | 835,000,000,000 | 44% |
| 60% | 1,020,000,000,000 | 54% |
| 70% | 1,180,000,000,000 | 62% |
| 80% | 1,400,000,000,000 | 74% |
| 90% | 1,570,000,000,000 | 83% |
| 100% | 1,900,000,000,000 |
As you can see the adjustments to the model assumption can have a fairly substantial impact on overall market gamma rates. Whats very interesting about these adjustments is that data shows (see chart below) when gamma is over ~$1bn its predicted impact effectively “tops out”. In other words a market with ~$1.5bn total gamma is anticipated to perform in the same way as a market with $2.5bn. For markets with >$1bn the model positioning assumptions could therefore be off by a fair amount and still “predict” the same estimated market return.
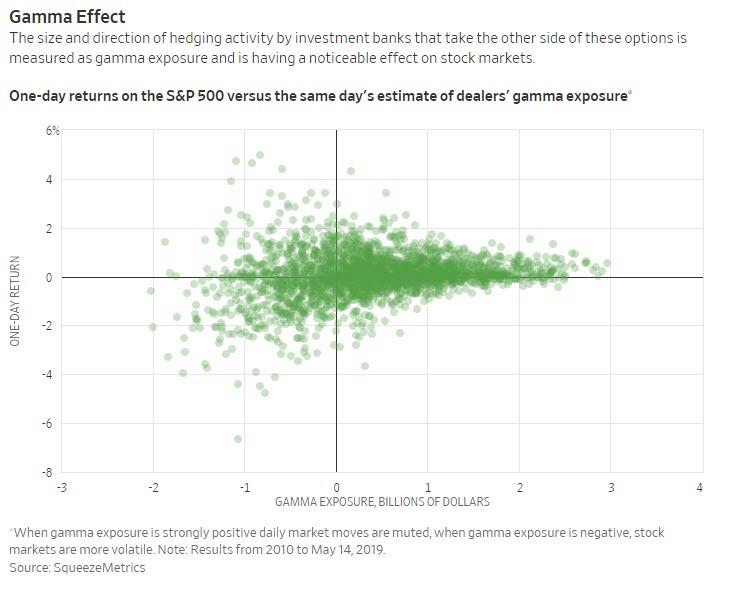
“Errors” in positioning assumptions for negative gamma periods would arguably matter less as we look for “high volatility” during negative gamma periods. High volatility does not predict direction, just magnitude of price movement. Therefore changes to underlying positions which in turn effect direction may not violate the models estimate of SPX movement.
A more in depth study of adjustment impacts to the position assumptions is certainly warranted.
Its also important to note that much like most traders and investors market gamma is but one key data points to consider, along with other large options-derived levels.
