For the past several months we have been analyzing a new method for monitoring stock market gamma we are calling the “SpotGamma Index.” Current market gamma measurements are an attempt to estimate the notional change in option market makers portfolios for a given move in the SPX index. This notional value is meant to be an estimate of options dealers hedging volume and in turn a method to estimate the impact of dealers in the futures market.
The SpotGamma Index seeks to estimate the change in portfolio value due to Gamma for a given change in SPX. The distinction is seemingly small, but the formula lends a bit more weight to sensitivity of the portfolio to S&P500 price movements. This appears to manifest in subtle changes, but at distinct moments.
We have gone through a rigorous testing process to ensure that this new measurement does not abandon the value of the current market gamma readings. Our goal was to enhance the metric, and make it more “user friendly”. Prior to releasing this data and providing the measurement for subscribers we did have several people examine and backtest the data.
The chart below shows positive gamma days in green vs negative in red.
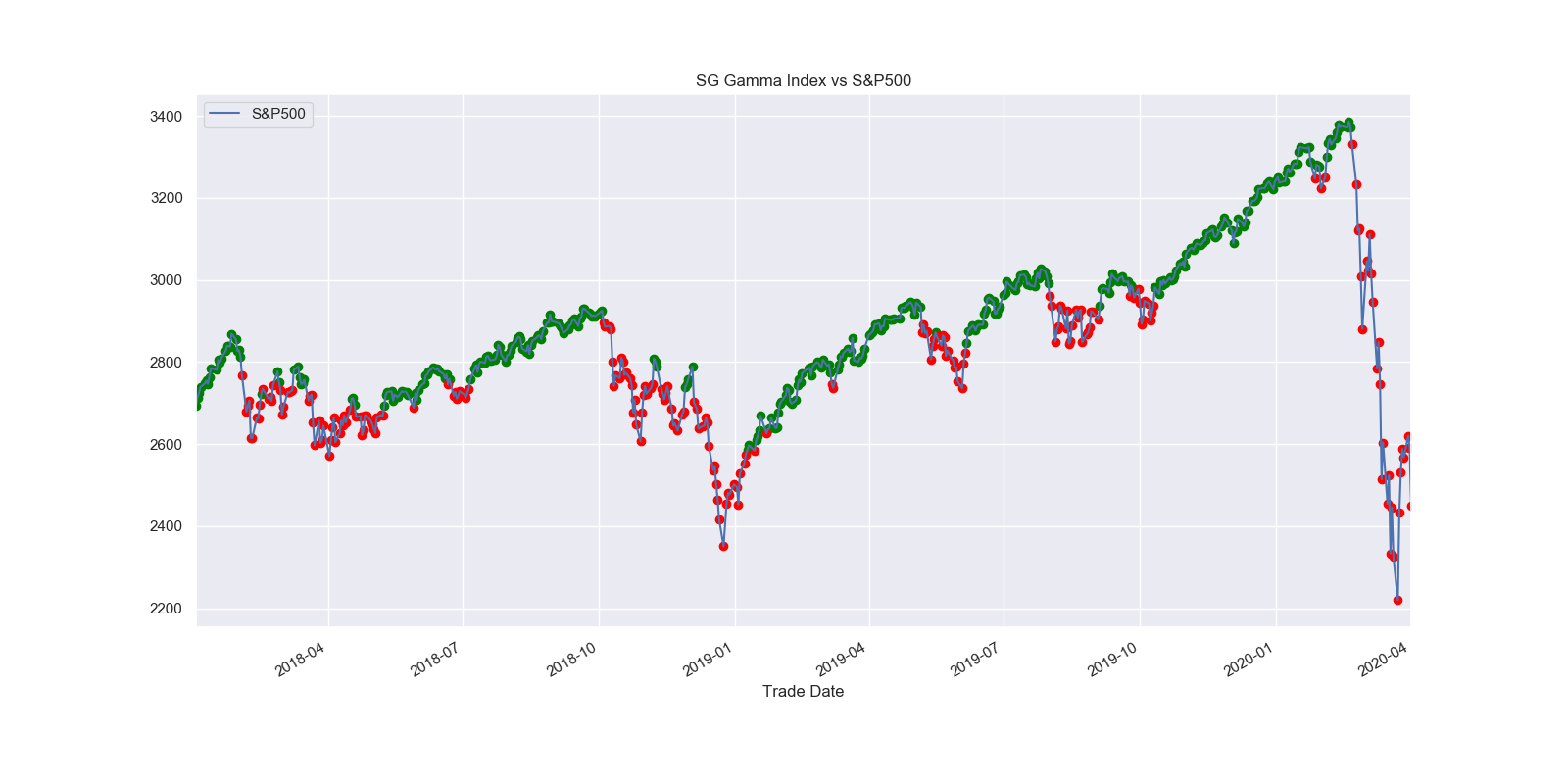
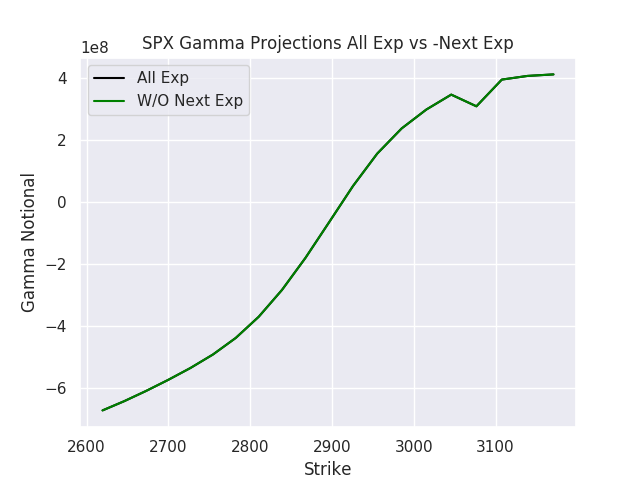
As you can see in the Gamma Curve below, the general distribution of gamma is very similar to current gamma estimates.
Gamma Statistics
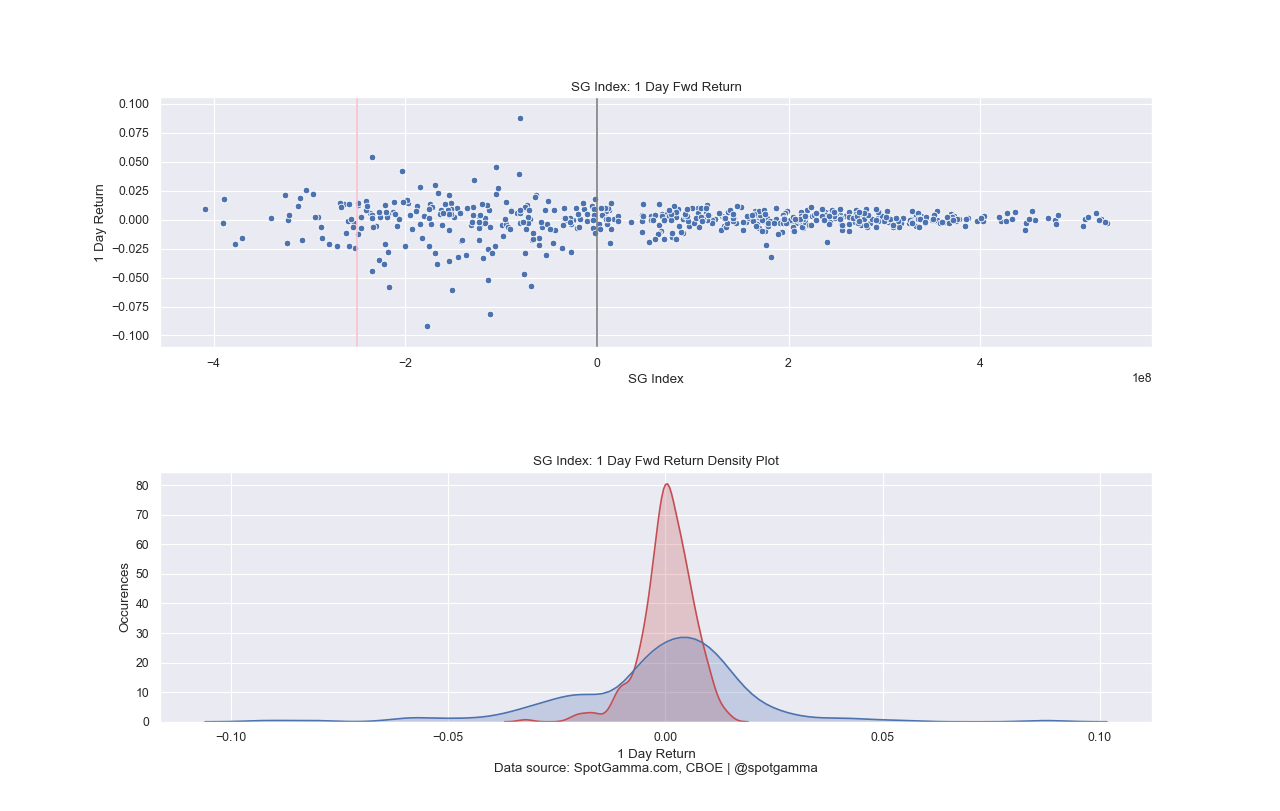
The charts below highlight two key graphics depicting the important but subtle changes in gamma using this updated formula. First we’d note the heteroscedastic nature of the SpotGamma Index is similar to that of typical “Gamma Notional” plots (see 3rd chart in green). The key differentiator is the expansion of volatility that seems to occur around zero gamma (black line, first chart).
If you compare this to the “Gamma Notional” scatter chart (3rd below in green) you can see that the similar expansion appears to occur more around the $1bn mark.
We are also very intrigued by what happens during extremely negative gamma movements (left of pink line in the chart below). We theorize that absolute returns are lower during these very negative gamma environments due to the risk tolerance of dealers during large drawdowns. Our belief is that dealers are long vega to protect tail risk and this may help in reducing volatility after large selloffs. Dealers must make markets and therefore cannot do much to limit their gamma exposure from expanding (i.e. getting more negative), but they can hedge against expanding volatility.
The chart below depicts the common “gamma notional” reading which seems to show volatility expansion around the $1 billion mark.
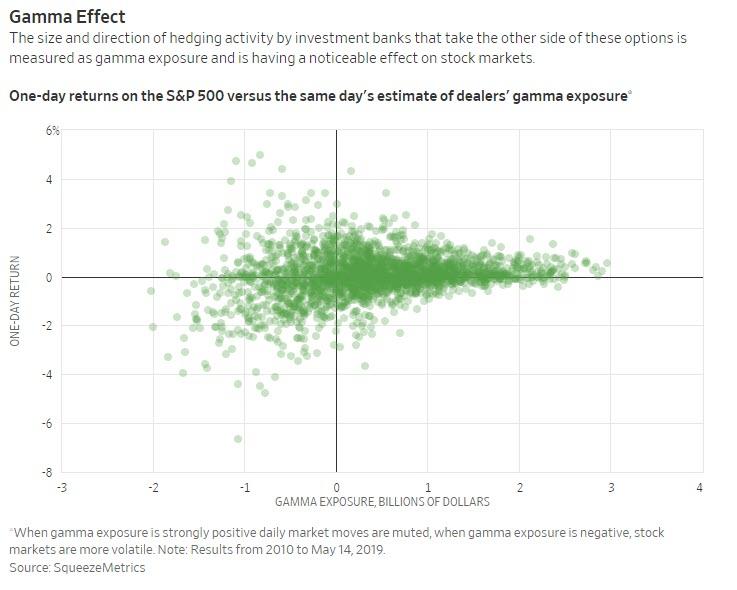
When someone quotes gamma as “$1 billion” that is generally meant to portray the notional amount that a dealer will have to buy or sell per point move in the S&P500 (via ES futures) . Functionally we believe this data has proven to be of great use, but with a few areas we felt could be further developed.
Practically speaking, quantifying gamma in such granularity seems to serve no purpose but has grown in nomenclature which we find a bit inconvenient. Accordingly we have decided to refer to the SpotGamma Index using an abbreviated two digit number which conveys the data in a more compact form.
